The effectiveness of a pseudo inverse extended born operator to handle lateral heterogeneity for imaging and velocity analysis applications
Abstract
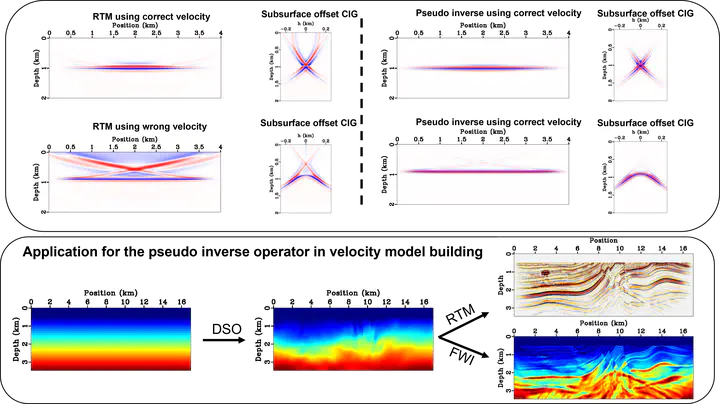
Wave equation–based migration velocity analysis techniques aim to construct a kinematically accurate velocity model for imaging or as an initial model for full waveform inversion applications. The most popular wave equation–based migration velocity analysis method is differential semblance optimization, where the velocity model is iteratively updated by minimizing the unfocused energy in an extended image volume. However, differential semblance optimization suffers from artefacts, courtesy of the adjoint operator used in imaging, leading to poor convergence. Recent findings show that true amplitude imaging plays a significant role in enhancing the differential semblance optimization’s gradient and reducing the artefacts. Here, we focus on a pseudo‐inverse operator to the horizontally extended Born as a true amplitude imaging operator. For laterally inhomogeneous models, the operator required a derivative with respect to a vertical shift. Extending the image vertically to evaluate such a derivative is costly and impractical. The inverse operator can be simplified in laterally homogeneous models. We derive an extension of the approach to apply the full inverse formula and evaluate the derivative efficiently. We simplified the implementation by applying the derivative to the imaging condition and utilize the relationship between the source and receiver wavefields and the vertical shift. Specifically, we verify the effectiveness of the approach using the Marmousi model and show that the term required for the lateral inhomogeneity treatment has a relatively small impact on the results for many cases. We then apply the operator in differential semblance optimization and invert for an accurate macro‐velocity model, which can serve as an initial velocity model for full waveform inversion.